An Example ARC Problem [2]
This article shares my attempt at the ARC challenge in 2024 [1]. As a spoiler, my results ended up being 3% accuracy on the private test set. While far from the 85% goal, I'm sharing this approach in hopes that it might be useful to others as a starting point or another way of thinking about the problem.
The goal of the arc challenge is to learn a transformation or program that transforms input grids to output grids, then apply that to a test grid. It is a unique benchmark in that each problem has unique transformations that have not been seen in previous examples. It tests general abstration and compositionality of an algorithm. Traditional machine learning and deep learning approaches don't work well on this challenge due to the fact that they require a dense sampling of samples to learn from. The ARC challenge is a very sparse sampling of the space of possible transformations.
An Example ARC Problem [2]
Although I tried many approaches, the one I ended up spending most of my time on was top down program synthesis via autoregressive search over a DSL based on the most likely next primitive in the abstract syntax tree. I utilized Michael Hodel's arc-dsl, which is a DSL for the ARC challenge. It consists of python functions such as rotations, flipping, and higher order functions such as map, filter, and reduce. Hodel also provide solutions for the training set of ARC.
I attempted to perform a discrete autoregressive search over the DSL that was inspired by the autoregressive inference process of LLMs. To make this clearer, any ARC dsl program can be represented as a tree where the nodes are functions or literals and the branches are parameters. An example solution to the problem #4c4377d9 is shown below:
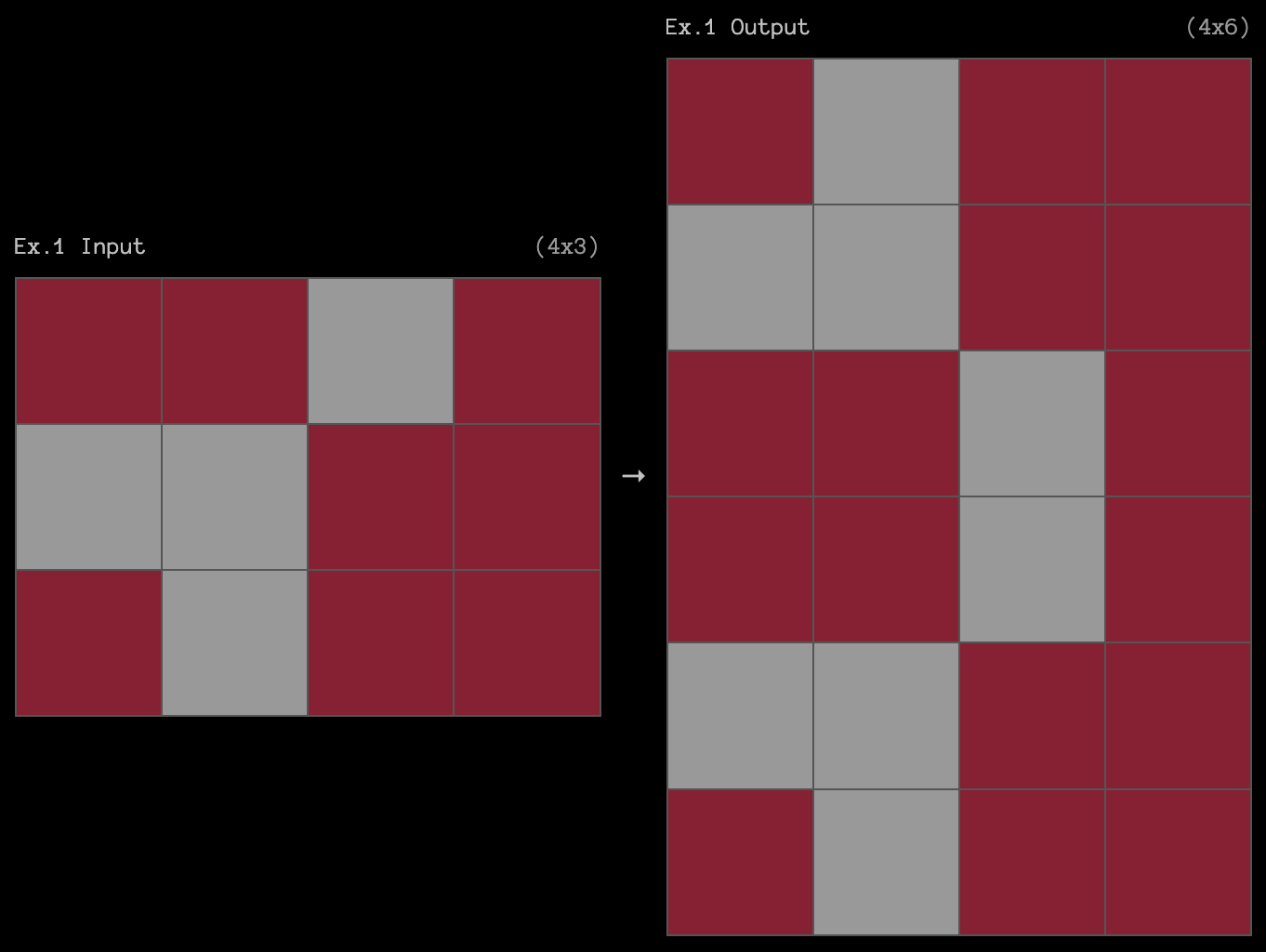Problem #4c4377d9 [1]
The solution to the problem can be written in code and tree form as follows:
def solve_4c4377d9(I):
x1 = hmirror(I)
O = vconcat(x1, I)
return O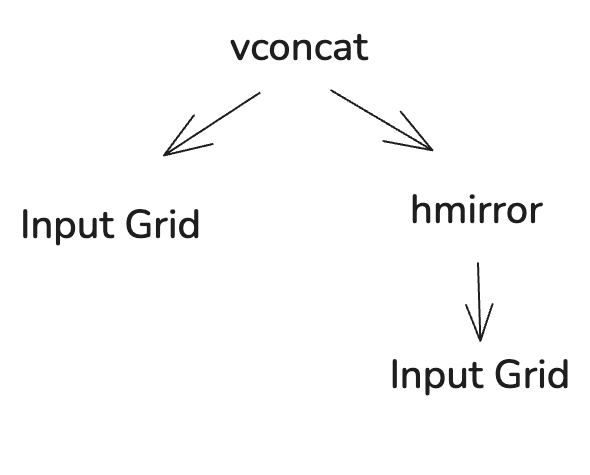
Given this tree structure, we can imagine that if we had a map of next token predictions like an LLM where the "token" is a function or literal, we could perform a search over the tree to find a solution. Given this approach we can select the most likely next token at each step and build a solution. A dummy example of this is shown below:
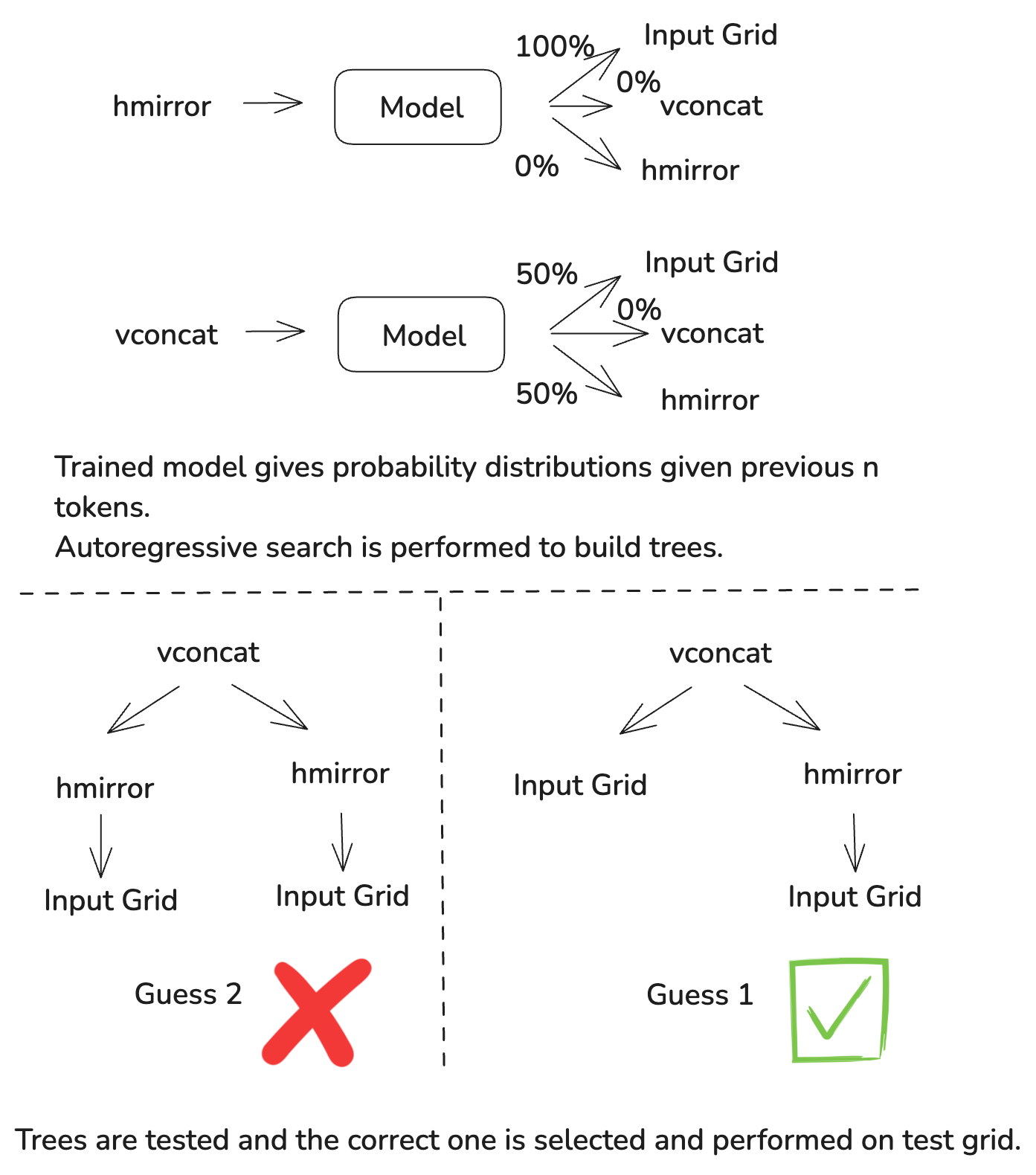
To train the model, I used the DSL solvers to generate datasets of each function to function/primitive transition and made a dataset using a single previous token to predict the next token as well as 2 previous tokens to predict the next token. Using any larger of a context window proved to be difficult with ARC becuase of such few examples, a large context window of previous DSL primitive overfits to the training set.
I used a combination of lookup tables and deep learning models for the predictive model. Lookup tables are much faster for program search than deep learning models so I used a deep learning model to "initialize" a lookup table and then used the lookup table for the search. The deep learning model would take in attributes of all the grids and a previous primitive and predict the next token primitive. Before the search, I would use the deep learning model to predict distribution for the next token for each primitive and persist it to a lookup table. This could then be used for fast search. The training for the deep learning model looked like the following:
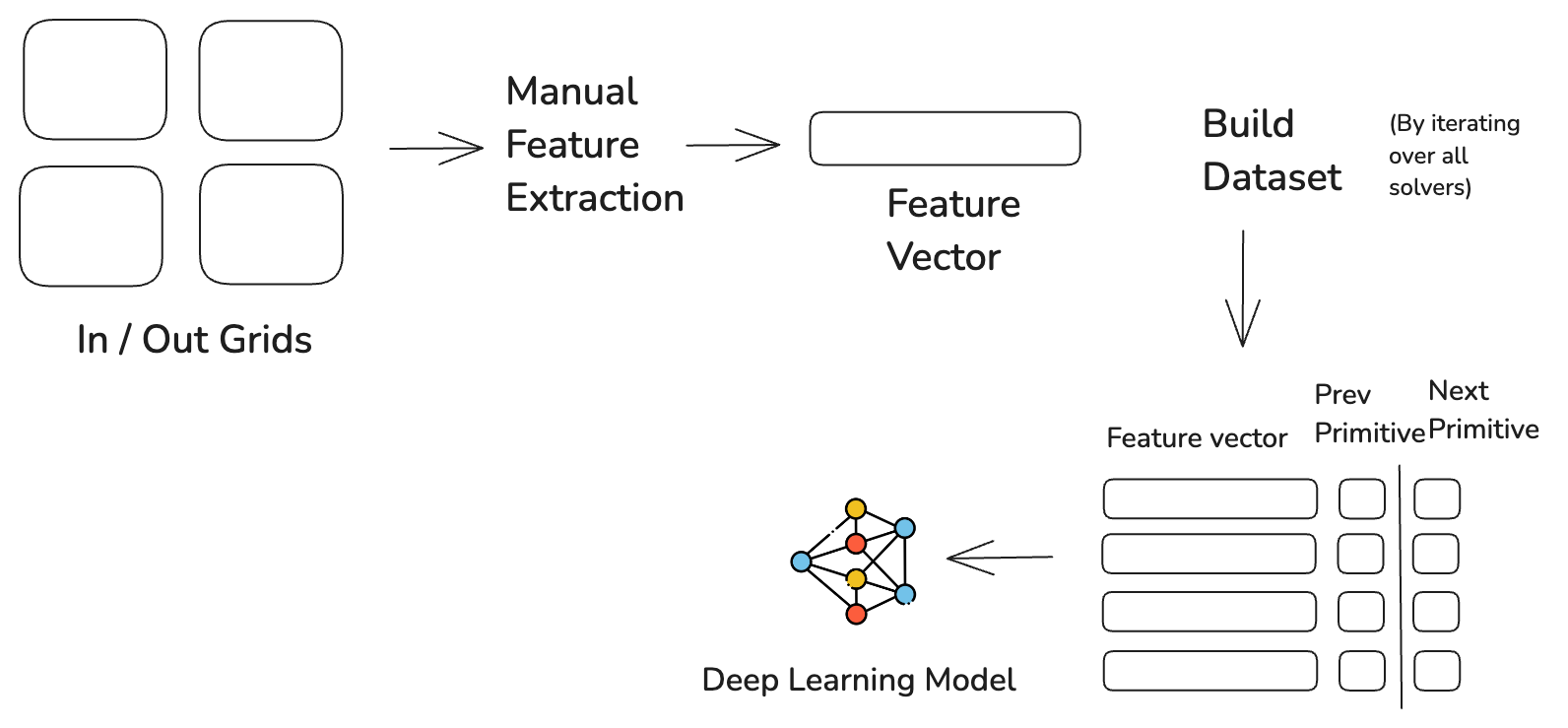
Once the deep learning model has been trained, it is used at the beginning of each problem search to initialize a lookup table.
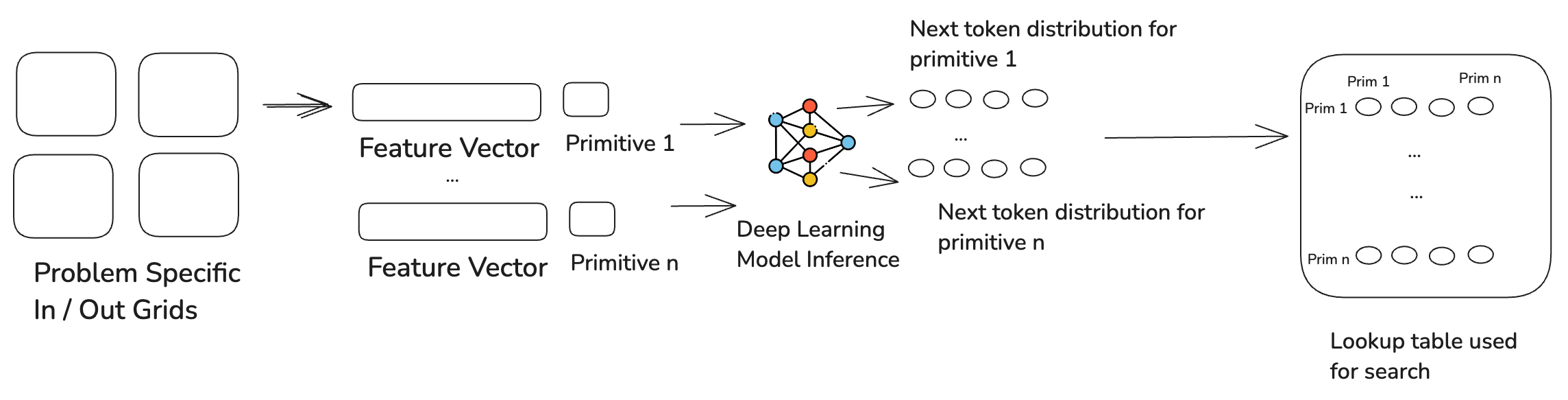
That lookup table is then used to generate up to 10000 trees and then selects a tree if it works on all three train grids. The attributes used to extract features from the grids and initialize the lookup table were 70 attributes. Most of the attributes are 1 or 0, 1 if the attribute is true for all the grids or 0 if it is not. A subset of the feature vector attributes are shown below:
Grid Objs Have 2D Volume Any (Out Grids)
Grid Objs Have 2D Volume Any (Difference of Grids)
Grid Objects Differ In Color (In Grids)
Grid Objects Differ In Color (Out Grids)
Grid Objects Differ In Color (Difference of Grids)
Grid Volume Distributed Upwards (In Grids)
Grid Volume Distributed Upwards (Out Grids)
Grid Strict Objs Are Volume One (In Grids)
Grid Strict Objs Are Volume One (Out Grids)
Grids Have At Least One Color On Edges (In Grids)
Grids Have At Least One Color On Edges (Out Grids)
Grids Have Frontiers (Out Grids)
Grids Have Frontiers (In Grids)
Grid Every Obj Has Gray Square (In Grids)
Grid Every Obj Has Gray Square (Out Grids)
Grids Have Object Dots (In Grids)
Grids Have Object Dots (Out Grids)
Grids Have Object Dots (Difference of Grids)
Grid Has Single Obj Multicolor (In Grids)
Grid Has Single Obj Multicolor (Out Grids)
Grid Has Single Obj Multicolor (Difference of Grids)
Grid Objs Have Mixed Colors (In Grids)
Grid Objs Have Mixed Colors (Out Grids)
Grid Objs Have Mixed Colors (Difference of Grids)
Grid Objs Have Mixed Diagonals (In Grids)
Grid Objs Have Mixed Diagonals (Out Grids)
Grid Objs Have Mixed Diagonals (Difference of Grids)
Grid Most Common Color Is Black (In Grids)
Grid Most Common Color Is Black (Out Grids)
Grid Most Common Color Is Black (Difference of Grids)
Grids Have Noise (In Grids)
Grids Have Noise (Out Grids)
All Objs Are Subset Palette Of Largest (In Grids)
All Objs Are Subset Palette Of Largest (Out Grids)
Grid One Obj Is Hsymmetric And Wide And Tall (In Grids)
Grid One Obj Is Hsymmetric And Wide And Tall (Out Grids)
....